
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ
Расстановка ударений: ИНТЕГРА`ЛЬНОЕ УРАВНЕ`НИЕ
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ воспроиз-ва населения, матем. уравнение, устанавливающее связь между числ. и возрастной структурой нас., с одной стороны, и возрастными интенсивностями рождаемости и смертности - с другой. Введено А. Дж. Лоткой в серии работ 1907-39. И. у. имеет вид:
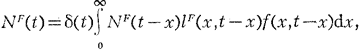
(1)
где N(t) - плотность распределения родившихся, т. е. число родившихся данного пола в период t1, t2 равно 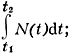
индекс F означает женский, а M - мужской пол, l(х, t) - функция дожития, т. е. вероятность для родившегося в момент t дожить до точного возраста х лет; f(x,t) - функция рождаемости, а f(x,t)Δ x - вероятность рождения ребёнка у женщины, родившейся в момент t, достигшей возраста х в интервале возрастов х, х + Δх; δ(t) - доля девочек среди родившихся в момент t, к-рая зависит, в частности, от возрастного состава рожающих женщин. Плотность распределения родившихся мальчиков равна:
NM(t) = (1 - δ(t))/δ(t)*NF(t) (2)
Плотность возрастной структуры нас. Р (х, t) находится из соотношений
PF(x,t) = lF(x,t - x)NF(t - x),
PM(x,t) = lM(x,t - x)NM(t - x). (3)
Числ. нас. в интервале возрастов x1, x2 в момент t равна
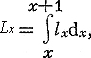
число родившихся девочек в момент t равно
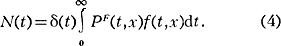
Уравнение (1) есть композиция соотношений (4) и (3) и наз. однородным И. у. Как видно из уравнения, чтобы определить N(t0) необходимо знать N(t) при t - β2
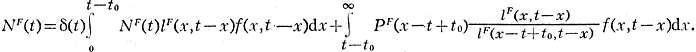
Соответственно изменяется уравнение (3) в случае, если t-x ≤t0.
P(x,t) = l(x,t -x)/l(x - t + t0, t - x) * P(x - t + t0,t0).
Обычно принимают, что δ(t) не зависит от времени (δ(t)= δ). Если допустить, что функции рождаемости и смертности не зависят от момента рождения, то уравнение (1) превращается в И. у. для стабильного населения.
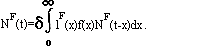
И. у. как элемент моделей воспроизводства населения применяется при анализе взаимозависимостей параметров режима воспроизводства населения.
Е. M. Андреев.
Источники:
- Демографический энциклопедический словарь/Гл.ред. Валентей Д.И. М.:Советская энциклопедия - 1985
|
ПОИСК:
|
© GEOGRAPHY.SU, 2010-2021
При использовании материалов сайта активная ссылка обязательна:
http://geography.su/ 'Geography.su: Страны и народы мира'

При использовании материалов сайта активная ссылка обязательна:
http://geography.su/ 'Geography.su: Страны и народы мира'