ЛОГИСТИЧЕСКОЕ НАСЕЛЕНИЕ

Расстановка ударений: ЛОГИСТИ`ЧЕСКОЕ НАСЕЛЕ`НИЕ

ЛОГИСТИЧЕСКОЕ НАСЕЛЕНИЕ (от греч. logistike - искусство вычислять, рассуждать), теоретич. модель нас., числ. к-рого меняется во времени в соответствии с уравнением логистич. кривой:

P(t) = K/(1 + e^{α - r}) (1)

где Р(t) - численность нас. в момент t, е - основание натурального логарифма; К, α, r - параметры формулы логистич. кривой. Концепция Л. н. впервые высказана А. Кетле (1835) и развита бельг. математиком П. Ферхюлстом (1838); в 20 в. исследована Р. Пирлом и Л. Ридом (США). В основе Л. н. лежит гипотеза 'насыщения', т. е. существования предельной для данных конкретных условий числ. нас., по мере приближения к к-рой рост нас. замедляется в силу влияния нек-рых препятствующих росту сил (см. рис.). Кетле писал, что 'сопротивление или сумма препятствий его [населения] увеличению, при прочих равных условиях, действует как квадрат скорости, с какой нас. имеет тенденцию роста'. Математически это условие записывается как

dP(t) = rP(t) - kP²(t)dt, (2)

где r - параметр, измеряющий прирост нас. за малый интервал времени, совпадает с параметром уравнения (1); k = r/K.

Решение уравнения (2) даёт (1).

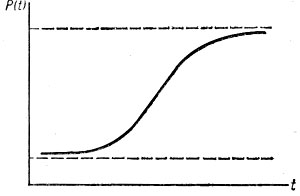
Кривая роста логистического населения

Логистич. кривая имеет определ. сходство с кривыми изменения числ. ряда нас. в ходе демографич. революции и применялась иногда для перспективных исчислений нас.; так, сов. учёный Г. Ф. Гаузе применил эту модель для прогноза числ. нас. СССР (1930). В дальнейшем выяснилось, что модель Л. н. не отражает динамики реальных нас. и, несмотря на попытки модернизации формулы (1), менее удовлетворительна, чем нек-рые др. методы демографич. прогноза. Модель Л. н. оказалась эффективной для описания роста нек-рых биол. популяций, предельный размер к-рых ограничен в силу ограниченности в зоне обитания к.-л. компонента, необходимого для нормальной жизнедеятельности её членов (т. н. лимитированные популяции).

Е. М. Андреев.

Источники:

1. Демографический энциклопедический словарь/Гл.ред. Валентей Д.И. М.:Советская энциклопедия - 1985