
ЭКСПОНЕНЦИАЛЬНОЕ НАСЕЛЕНИЕ
Расстановка ударений: ЭКСПОНЕНЦИА`ЛЬНОЕ НАСЕЛЕ`НИЕ
ЭКСПОНЕНЦИАЛЬНОЕ НАСЕЛЕНИЕ (от лат. exponens - показывающий), матем. модель, описывающая нас. с постоянными во времени темпом роста и одним из двух параметров его воспроиз-ва: возрастной структурой или функцией дожития.
Среди простейших моделей, определяющих тенденцию изменения общей числ. нас., выделяются те, к-рые учитывают только постоянный темп роста. Если N(t) - общая числ. нас. в момент t, то динамика Э. н. имеет вид: N(t) = N(0)ert, где N(0) - начальная числ. нас., r - коэфф. естеств. прироста, е - основание натуральных логарифмов. При r>0 или r<0 числ. нас. увеличивается или уменьшается согласно экспоненциальному закону. Если r = 0, то общая числ. нас. остаётся постоянной. Однако в такой модели ничего не известно о возрастной структуре и параметрах воспроиз-ва - рождаемости и смертности. Поэтому в совр. понимании Э. н. учитывает не только r, но также один из постоянных параметров режима воспроиз-ва. В этом смысле модель Э. н. была впервые введена в демографию А. Дж. Лoткой (1907) и, независимо от него, В. И. Борткевичем (1911). При этом Лотка пользовался термином 'мальтузианское население', к-рый получил распространение в зарубежной лит-ре. Э. н. занимает центральное место в теории стабильного населения, поскольку позволяет аналитически выразить осн. взаимосвязи между параметрами воспроиз-ва на основе интегрального уравнения типа уравнения Вольтерра: 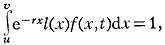
где u и v - начальный и конечный возраст репродуктивного периода, l(x) - функция дожития, r - темп роста, f(x, t) - функция рождаемости.
Франц. ученый Ж. Буржуа-Пиша предложил два метода классификации множества Э. н. Первый метод учитывает заданную функцию дожития 1(х) и оп ределённое значение r. Формулы, выражающие зависимость между r и l(x), дают возможность вычислить осн. характеристики Э. н. При этом доля женщин С(х) в возрасте от x до x + dx будет равна
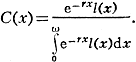
Общий коэфф. рождаемости.
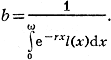
Др. метод классификации множества Э. н. заключается в сочетании определенного возрастного состава нас. С(х) с нек-рым заданным значением r. В этом случае имеет место аналитич. зависимость между r и С(х), к-рая позволяет вычислить недостающие характеристики Э. н. При этом общий коэфф. рождаемости: b = С(0); функция дожития l(x) = C(x)/C(0)*erx.. Отсюда интегральное уравнение воспроиз-ва принимает вид 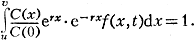
В результате преобразований имеем: 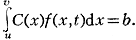
Введение в Э. н. заданной функции рождаемости f(x) приводит к единств. модели, в к-рой произвольный параметр r заменяется расчетным ρ - действительным корнем интегрального уравнения воспроиз-ва. Такую модель Э. н. Лотка назвал стабильным нас., соответствующим функциям l(x) и f(x).
Первоначально Э. н. рассчитывалось только для женского нас. С сер. 40-х гг. 20 в. было сделано обобщение для обоих полов. В этом случае Э. н. можно определить как нас., в к-ром постоянны, а) доля рождений мальчиков; б) три из следующих 4 функций, функция дожития женщин; распределение женщин по возрасту; функция дожития мужчин, распределение мужчин по возрасту.
Пирожков С. И., Демографические процессы и возрастная структура населения, М. 1976; Таба Л., Взаимосвязи между возрастной структурой, плодовитостью, смертностью и миграцией. Воспроизводство и обновление населения, пер. с англ., в кн. Демографические модели, М. 1977, Буржуа-Пиша Ж., Стабильные, полустабильные населения и потенциал роста, пер. с англ. там же.
С. И. Пирожков.
Источники:
- Демографический энциклопедический словарь/Гл.ред. Валентей Д.И. М.:Советская энциклопедия - 1985
|
ПОИСК:
|
© GEOGRAPHY.SU, 2010-2021
При использовании материалов сайта активная ссылка обязательна:
http://geography.su/ 'Geography.su: Страны и народы мира'

При использовании материалов сайта активная ссылка обязательна:
http://geography.su/ 'Geography.su: Страны и народы мира'