О масштабах

Читать карту, не зная масштаба, это все равно что читать рассказ, не зная, где и когда происходят события. И тем, кто еще не научился им пользоваться, необходимо знать, что чем мельче масштаб, тем более обширное пространство может быть показано на листе карты, но местность на ней изображается с меньшими подробностями, и наоборот, чем крупнее масштаб карты, тем с большей детальностью могут быть показаны на ней элементы ее содержания.

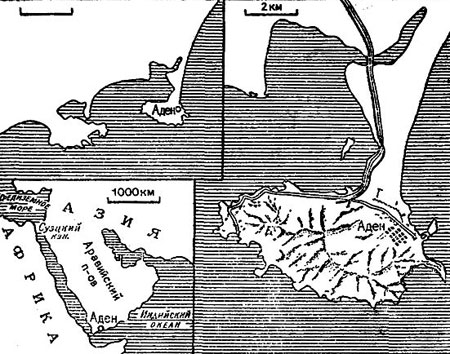
Рис. 17. Картографическое изображение в разных масштабах

Часто для иллюстрации обзорных статей в газетах и журналах приводятся две или даже три карты разных масштабов. Это дает возможность читателю рассмотреть во всех подробностях небольшую страну или ее часть и в то же время узнать ее местоположение на карте мира. В качестве примера на рис. 17 приводятся три вырезки из карт разных масштабов, на которых расположен город Аден. Справа дана карта самого крупного масштаба: в 1 см 2 км. На ней показано подробное изображение города, ведущие к нему дороги и даже рельеф местности. Слева внизу показана обзорная карта очень мелкого масштаба: в 1 см 1000 км. Здесь мы можем познакомиться с местоположением Адена относительно частей света, морей и океанов. Слева вверху дана карта, на которой подробно отображено прилегающее побережье на десятки километров, но ее масштаб все же не позволил изобразить местность с такой подробностью, как на правой карте. Здесь мы обозначили масштабный отрезок размером 1 см, но не подписали, чему он соответствует. Попытайтесь сами определить это значение, т. е. узнать масштаб карты.

Для решения задачи измерьте на верхней левой карте ширину и длину Аденского полуострова в миллиметрах и сравните их с соответствующими расстояниями на правой карте. Если вы правильно сделали, то расстояния получатся в пять раз меньше. Значит, и масштаб ее будет в 5 раз мельче правой карты, т.е. в 1 см 10 км.

Масштабы карт обычно выражают отношением единицы к числу, показывающему, во сколько раз все размеры на карте меньше соответствующих размеров в натуре. Вот, например, два масштаба: 1:500000 и 1:10000000. Сообразите, какой из них крупнее и во сколько раз.

Более крупным считается тот масштаб, в котором одни и те же географические объекты изображаются крупнее. В самом деле, масштаб представляет собой дробь, в числителе которой единица. А из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель. Значит масштаб 1:500000 крупнее масштаба 1:10000000 в 20 раз.

А если вам встретится такое выражение: «Масштаб карты более 1 км в 1 см», что же это будет за карта? Крупнее или мельче, чем карта масштаба 1: 100000, у которой 1 см точно соответствует 1 км? Оказывается мельче, потому что, чем больше знаменатель, тем мельче масштаб карты.

По численному масштабу очень легко узнать именованный масштаб (число километров, соответствующее 1 см карты). Километр, как известно, содержит 10ООООсм. Значит, знаменатель масштаба надо разделить на 100000, т.е. у знаменателя нужно зачеркнуть последние пять нулей.

В топографии мы привыкли считать масштаб для всего листа карты величиной постоянной. На мелкомасштабной карте, изображающей значительную территорию, масштаб непостоянен. Он бывает различен не только в разных частях карты, но и в различных направлениях в зависимости от проекции.

Необходимость иметь дело с переменным масштабом усложняет пользование картой. Для удобства работы картографы задают так называемый главный масштаб, который соответствует масштабу в каких-либо определенных местах проекции. Такими местами могут быть точки или линии касания поверхностей, на которые проектируется градусная сетка с глобуса на карту. Значит, чтобы определить главный масштаб карты, нужно, прежде всего, знать, в какой проекции она составлена.

Обратимся к рис. 13. Все три карты, представленные на нем, составлены в цилиндрических проекциях, а для них характерно касание цилиндра по линии экватора. Следовательно, на экваторе и будут главные масштабы для наших карт. Нетрудно догадаться, что в данном случае все карты имеют один и тот же главный масштаб, так как промежутки между двадцатиградусными меридианами везде равны и составляют 3 мм. Можно определить и величину главного масштаба. Известно, что дуга экватора в 10° на земном шаре равна 1113 км. Этому расстоянию соответствует на карте отрезок, равный 0,3 см. Значит, в одном сантиметре карты содержится примерно 3700 км (1113:0,3), и численный масштаб составляет 1:370000000.

Кроме главного масштаба каждая карта имеет частные масштабы. Их можно выражать в обычном виде или в долях от главного масштаба, например 0,9, 1,1 и т. п.

На карте в квадратной проекции (см. рис. 13,6) частный масштаб по всем меридианам на всем их протяжении одинаковый и равен главному. На карте в равноугольной проекции (см. рис. 13, а) он постепенно увеличивается от экватора к полюсу, а на карте равновеликой проекции (см. рис. 13,в), наоборот, уменьшается. Частный масштаб по параллелям на всех трех картах по мере приближения к полюсу резко возрастает, а на самом полюсе им бессмысленно пользоваться, ибо точка, обозначающая полюс, «растянулась» на всю ширину земной поверхности.

Определим частные масштабы для наших карт по 60-й параллели. Чтобы решить такую задачу, нужно знать длины дуг параллелей на разных широтах. Значения их в 5 и 10° (в скобках) приведены в табл. 1.

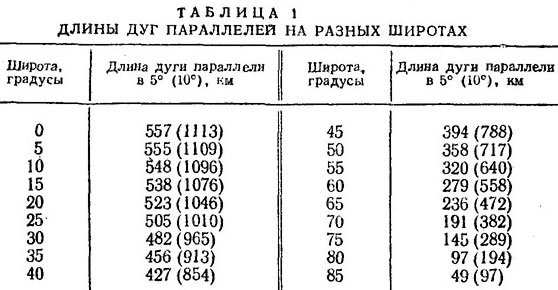
Длины дуг параллелей на разных широтах

Частный масштаб по 60-й параллели на всех трех картах будет один и тот же, ибо отрезки параллелей, заключенные между меридианами, равны и соответствуют так же, как и по экватору, 0,3 см. Возьмем из таблицы значение длины дуги параллели в 10° на широте 60° и, разделив ее на 0,3, получим именованный масштаб или, как еще говорят, величину масштаба, равную 1860 км в 1 см (558:0,3). Частный масштаб, выраженный в долях к главному, будет составлять примерно 2,0 (3700:1860).

Таким путем частный масштаб можно определить лишь в том случае, когда он остается постоянным по данному направлению. Если же масштаб изменяется, то у нас получится средняя его величина. Например, на карте в равноугольной проекции (см. рис. 13, а) на каждом бесконечно малом отрезке меридиана будет иметь свой частный масштаб. Понятно, что практически пользоваться им нельзя. Но можно сопоставить отрезки по меридиану между какими-то параллелями. Например, отрезок между 60 и 70-й параллелями в два раза больше, чем у экватора. Значит, на этом отрезке средний масштаб крупнее главного в два раза.

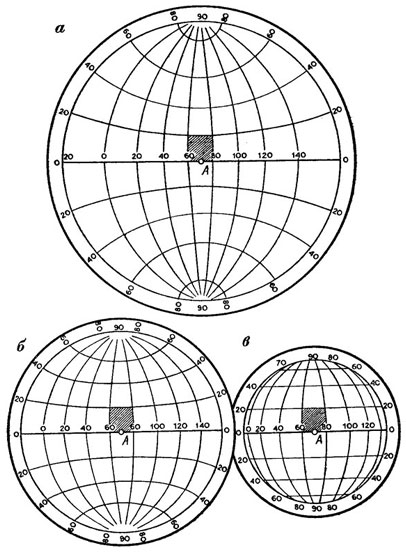
Рис. 18. Картографическая сетка полушария в трех проекциях: а - равноугольной; б - равновеликой; в - произвольной

В картографической практике не принят термин «средний масштаб», и на всех картах подписывают только главный масштаб. Для тех, кто пользуется картой, главный масштаб не всегда понятен, так как часто не выражает общей масштабности изображения. Обратимся к рис. 18, на котором показано полушарие в трех различных проекциях: равноугольной (стереографической), равновеликой и произвольной (ортографической). Все три проекции азимутальные экваториальные, так как картографическая сетка во всех случаях перенесена на плоскость, касательную в точке экватора. Эта точка А называется точкой нулевых искажений, и для нее указывают и подписывают на карте главный масштаб. Несмотря на различные размеры полушарий, главный масштаб всех трех проекций получился одинаковым. В этом нетрудно убедиться. Возьмем клетку картографической сетки, расположенную в районе точки А. В первом приближении она имеет форму трапеции, и размеры ее во всех проекциях примерно одинаковы. Измерим основания трапеции, т.е. отрезки экватора, ограниченные ближайшими к точке А меридианами. Они получаются равными 0,6 см. Расстояние по экватору, соответствующее этому отрезку, т.е. дуге в 20°, составляет 2220 км. Значит, масштаб в центральной части каждой проекции, соответствующий примерно главному масштабу, будет равен 1:370000000 (в 1 см 370 км). Такой масштаб и был бы подписан на всех трех картах, несмотря на разные размеры полушарий. Это удобно картографам, так как главный масштаб математически обоснован, и они используют его как основу для расчета и составления проекций. Для нас же более наглядным и практичным был бы средний масштаб по каким-либо линиям или направлениям. В данном случае средний масштаб по экватору для стереографической проекции равен 1:286000000, а для ортографической - 1:572000000 (в два раза мельче).

На картах обычно дается не только численный, но и линейный масштаб в виде графической шкалы. Понятно, что для карты определенного масштаба строят соответствующую шкалу. Но можно построить и один график для карт разных масштабов.

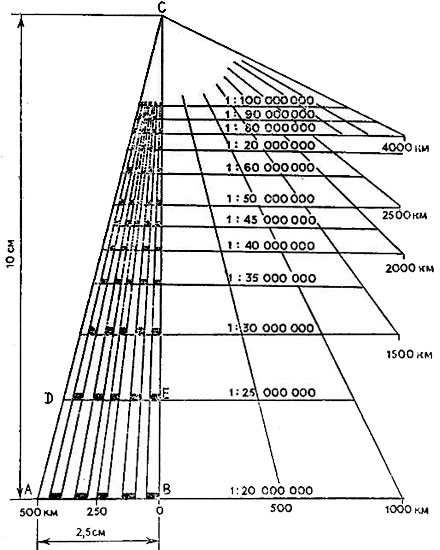
Рис. 19. Универсальный масштаб

Проведем две взаимно перпендикулярные линии и отложим по вертикальной оси вверх отрезок ВС, равный 10 см, а по горизонтальной оси влево - отрезок ВА, равный 2,5 см (рис. 19). Этот последний отрезок будем считать основанием линейного масштаба для карты 1:20000000. В этом масштабе он будет соответствовать 500 км. Чтобы найти расстояние СЕ, от которого нужно отложить основание следующего масштаба (1:25000000), пользуются соотношением, полученным из подобия треугольников ABC и ADE:

CB/CE=AB/DE; CE=(CB*DE)/AB=10DE/2,5=4DE.

Величина DE - основание линейного масштаба - для карты 1:25000000 соответственно будет равна 2 см (500км:25000000), значит СE=8см. Так же рассчитывают расстояния от точки С до линий, где будут строиться основания линейных масштабов других карт.

Построенный график можно использовать не только для измерения расстояний по картам разных масштабов, но и для определения среднего масштаба по любому меридиану и любой параллели. Масштаб карты по меридиану определяют в следующем порядке. Раствор циркуля-измерителя, соответствующий отрезку меридиана с разностью широт 5 или 10°, будем вести по нашему масштабу вдоль наклонных линий до тех пор, пока он не уложится в расстояние 555 км для 5° или расстояние 1110 км для 10° на какой-либо горизонтальной линии. Масштаб, подписанный над этой линией, будет соответствовать среднему масштабу карты по данному меридиану. Например, отрезок MN, снятый с карты по меридиану с разностью широт 10°, уложился в расстояние 1110 км по линии масштаба 1:40000000. Таков и будет средний масштаб карты в данном направлении.

Чтобы определить масштаб карты по параллели, нужно вначале найти по приведенной выше таблице длину дуги параллели в 5 или 10° на определенной широте, а затем порядок действий будет тот же, что и при определении масштаба карты по меридиану.