Как искажаются материки на карте

При изображении на плоскости географических объектов, расположенных на сферической поверхности, неизбежны искажения. На картах характер искажений зависит от вида проекции. На одних сильно меняются размеры площадей, но сохраняется равенство углов. Такие проекции называют равноугольными. Другие карты, наоборот, отличаются тем, что сохраняют размеры площадей, но сильно искажают конфигурацию материков. Это так называемые равновеликие проекции. Но многие карты имеют проекции, которые хотя и обладают своими видами искажений, однако каждое из них остается сравнительно малым. Такие проекции называются произвольными.

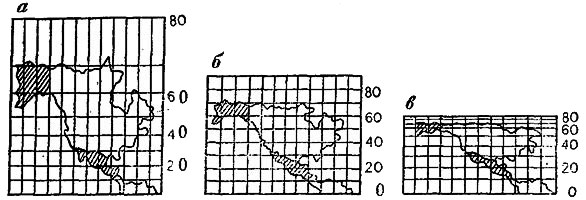
Рис. 13. Карта Северной и Центральной Америки в трех проекциях: а — равноугольной; б — произвольной; в — равновеликой

На рис. 13 приведены карты Северной и Центральной Америки, составленные в знакомых нам цилиндрических проекциях Меркатора, Ламберта и Энрико. Проекция Меркатора (рис. 13, а) равноугольная. На ней сохраняются направления, а, следовательно, и конфигурация береговых линий в отдельных ее частях, но сильно искажаются площади по мере удаления от экватора, Площадь Аляски, например, вышла на карте в два раза больше Мексики. Между тем в действительности территория Мексики больше территории Аляски. Проекция Ламберта (рис. 13, в) - равновеликая. Здесь сохраняется соотношение площадей, но в значительной мере искажены углы. В результате конфигурация северных берегов материка настолько изменена, что стала совсем не похожей на действительную. По виду искажений квадратную проекцию (рис. 13,6) следует отнести к произвольной, так как ей свойственны и угловые и площадные искажения, но в меньшей степени, чем в двух других.

Остановимся более подробно на карте в проекции Меркатора. В квадратной проекции искажения контуров материков особенно заметны потому, что при сохранении единого масштаба вдоль меридианов масштаб по параллелям нарастает и достигает огромных размеров вблизи полюсов. Меркатор решил пропорционально растяжению параллелей между меридианами увеличивать и отрезки самих меридианов. В этом случае, хотя и пришлось поступиться сохранением единого масштаба вдоль меридианов, все же удалось сохранить подобие фигур небольших участков земной поверхности, их действительные, неискаженные очертания. А в подобных фигурах углы остаются соответственно одинаковыми. Понятно, что при переходе к большим фигурам подобие и здесь нарушалось.

Итак, Меркатор дополнительно растянул отрезки меридианов в определенной последовательности: чем ближе к полюсу, тем большее растяжение испытывает отрезок меридиана. У полюсов меридианы становятся бесконечно длинными, и поэтому Меркатор был вынужден срезать карту сверху и снизу, отбросив приполярные области. Кстати очертания их тогда были известны крайне неточно и неполно, и спроса на карты этих территорий, естественно, не было.

Карта Меркатора особенно облегчала решение штурманских задач. Угол, измеренный на ней между направлением меридиана и направлением на конечный пункт, точно соответствует курсу корабля. Корабль вели по компасу, а если углы между меридианом и направлением пути, как на карте, так и на поверхности Земли совпадают, значит, штурман может быть уверен в правильности курса. Но будет ли по этому направлению проходить кратчайший путь?

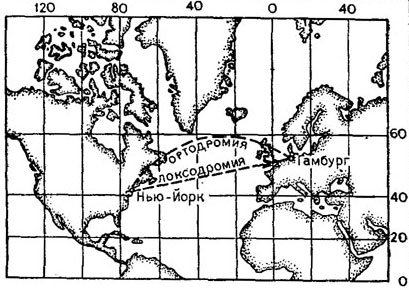
Рис. 14. Локсодромия и ортодромия на карте в проекции Меркатора

Перед нами карта в проекции Меркатора (рис. 14). Попытаемся нанести на нее кратчайший путь, например, из Гамбурга в Нью-Йорк. Соединим оба города прямой линией. На первый взгляд можно сказать, что по этой линии, которую называют локсодромией, и будет проходить кратчайший путь. Ведь это прямая линия, а что может быть короче прямого пути. Но это не так: на самом деле кратчайшее расстояние между Гамбургом и Нью-Йорком соответствует длине кривой линии, называемой ортодромией. На шаре это дуга большого круга, на эллипсоиде - более сложная кривая. Расстояние по локсодромии на поверхности земного шара всегда больше расстояния по ортодромии, за исключением направлений по меридиану и экватору, где локсодромия одновременно является и ортодромией. На рисунке показаны локсодромия и ортодромия, соединяющие Гамбург с Нью-Йорком. Как видите, кратчайшее расстояние между этими городами на карте в проекции Меркатора окажется кривой линией - ортодромией. В этом нетрудно убедиться, натянув на глобусе нить между заданными пунктами. Натянутая нить - бесспорный указатель кратчайшего пути. Именно по ортодромической трассе совершили в 1939 г. перелет Москва - Нью-Йорк Герой Советского Союза В. К. Коккинаки и штурман М. Гордиенко.

Впервые прокладку курса по кратчайшему пути разработал в 1731 г. русский ученый, крупнейший исследователь Сибири и Арктики С. Г. Малыгин. Он составил специальную карту, по которой можно нанести ортодромию. Пользуясь картой Малыгина, корабль вели с помощью компаса кратчайшим путем, но в расчетный курс через определенные интервалы вводили поправки. Малыгин разработал не только карту, но и методику определения поправок в расчетные курсы и составил для этой цели специальные таблицы.

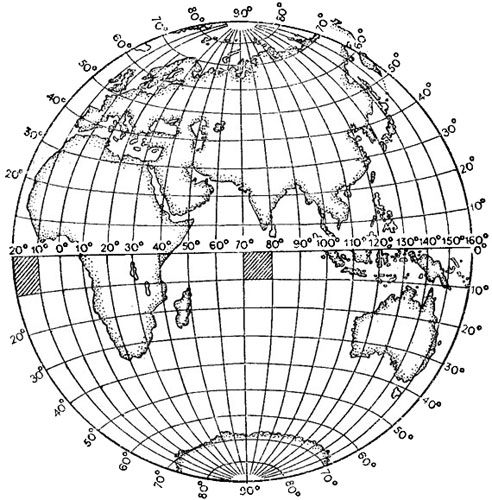
Рис. 15. Карта полушария в равновеликой проекции Ламберта

В отличие от проекции Меркатора проекция Ламберта (см. рис. 13, в) сохраняет правильное соотношение площадей материков, морей и др. Ламберт составил также в равновеликой проекции и карты полушарий. По начертанию параллелей и меридианов эта проекция относится к поперечной азимутальной (рис. 15). Искажения конфигурации материков на карте полушарий в проекции Ламберта значительны. В этом можно убедиться, рассматривая очертания участков земной поверхности протяженностью 10е по широте и 10° по долготе. На глобусе все такие участки, расположенные на одной и той же широте, равны между собой, а на карте начертания на разных долготах различны. Если у экватора в середине полушария клетка градусной сетки имеет форму квадрата, то к краям карты она сильно вытянута по долготе и сужена по широте. Подобные искажения градусной сетки наблюдаются и на любых других широтах.

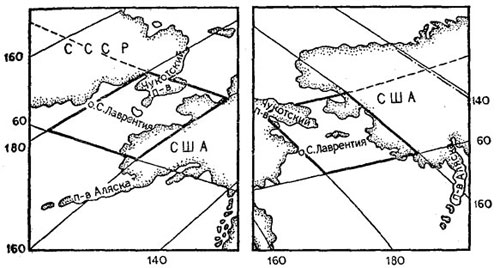
Рис. 16. Изображение Чукотки и Аляски в различных углах карты

Из карты двух полушарий можно составить одну карту мира, которая также имеет свойство равновеликости. Для этого проделаем следующее. На одном из полушарий у пересечения экватора со средним меридианом, имеющим вид прямой линии, подпишем нуль, а вправо и влево от этой точки по экватору дадим оцифровку меридианам через 20° (0, 20, 40,..., 180°). Получилась картографическая сетка для карты мира. Но если бы мы поместили в этот круг изображения материков с обоих полушарий, то свойство равновеликости было бы нарушено. Чтобы оно сохранилось, нужно из окружности сделать овал, уменьшив вдвое промежутки между параллелями по среднему меридиану. Такую проекцию впервые составил русский ученый-картограф Д. А. Аитов. Равновеликие проекции часто применяют для составления политической карты мира, так как на ней очень важно показать правильное соотношение площадей различных стран. Политическая карта обычно бывает не в овальной рамке, а в прямоугольной, и в ее углах повторяют изображения одной и той же территории. Такие изображения, вырезанные из северо-западного и северо-восточного углов карты, представлены на рис. 16. На правой и левой вырезках выделена клетка градусной сетки, ограниченная двумя одноименными меридианами (180 и 160° з.д.) и параллелями (60° с. ш. и Северным полярным кругом). Соответствующие стороны обеих клеток имеют почти одинаковые размеры, и поэтому площади одноименных островов и полуостровов на той и другой вырезке будут равны. Вместе с тем искажения в направлениях очень велики. Если на левой вырезке угол между параллелью и меридианом острый, то на правой вырезке он тупой, и наоборот. Соответственно искажены и углы с любого пункта на однозначные объекты. Все это сказывается на конфигурации полуостровов, островов, рек. Сравните, например, изображения Аляски на правой и левой вырезках из карт. Они настолько непохожи друг на друга, что на первый взгляд их трудно сопоставить. Обратите внимание на остров Святого Лаврентия. На левой вырезке он сплюснут, а на правой - вытянут, и нет никакого подобия между этими двумя изображениями одного и того же острова. Для большинства карт применяют произвольные проекции, которые не дают резких искажений в очертаниях материков и их площадей. Поэтому в таких проекциях обычно составляют большую часть карт мира.