Градусная сетка на карте

Градусная, или, как называют ее составители карт, картографическая, сетка служит не только основой для нанесения элементов ландшафта, но и наглядно передает кривизну изображаемой поверхности, особенно на мелкомасштабных картах. Градусная сетка позволяет определить масштаб, когда он не обозначен (дуга одного градуса меридиана в средних широтах СССР равна 111 км), или проверить его, когда он вызывает сомнение. Учитывая свойства проекции, градусной сеткой можно пользоваться для измерения расстояний и площадей. Наконец, градусная сетка позволяет определить на карте географические координаты любого пункта или нанести пункт по его координатам.

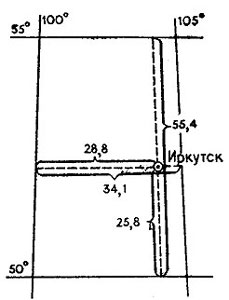
Рис. 31. Схема измерения отрезков для определения географических координат

Допустим, нам надо определить координаты города Иркутска (рис. 31). Найдем градусную клетку, где расположен город, и узнаем широты нижней и верхней параллелей, а также долготы левого и правого меридианов. Через центр условного знака города проведем линии, параллельные ближайшим меридиану и параллели. По этим линиям измерим расстояния между меридианами и параллелями, а также расстояния от меридиана и параллели до нашего пункта. Для определения широты пункта составим и решим пропорцию:

55,4 мм - 5°; Χ=(25,8*5)/55,4 = 2,3°.

25,8 мм - Χ;

Широта пункта получилась равной 52,3° в. д. Аналогично вычисляют и долготу.

Значительно проще, хотя с несколько меньшей точностью координаты определяют по градусным шкалам, расположенным на сторонах внешней рамки карты. Чтобы определить широту какого-либо пункта, возьмем раствором циркуля расстояние от него до верхней параллели клетки градусной сетки, в которой находится пункт.

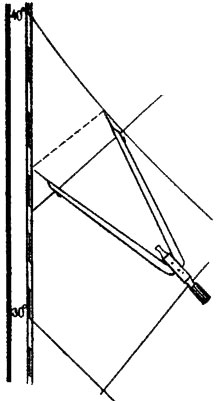
Рис. 32. Определение географической широты по градусной сетке

Приложим этот раствор к западной или восточной стороне рамки так, чтобы одна игла помещалась на градусной шкале, а вторая - в точке касания параллели, до которой измеряли расстояние, и произведем по шкале отсчет. В примере на рис. 32 широта самого южного пункта нашей страны - Кушки получилась равной 35,3°. При отсутствии циркуля-измерителя можно воспользоваться линейкой или полоской бумаги. Долготу пункта можно определить с помощью линейки. Ее прикладывают так, чтобы прямая линия проходила через заданную точку и одинаковые долготы на северной и южной сторонах рамки. Отсчет долготы в северном полушарии лучше делать по шкале на южной стороне, так как интервалы там больше и отсчеты получаются точнее.

Пункты по заданным координатам наносят на карту в обратном порядке. В качестве примера решим такую задачу. Экспедиция О. Ю. Шмидта высадилась на лед с затонувшего «Челюскина» 13 февраля 1934 г., 15 февраля Э. Т. Кренкель дал радиограмму: «Второй день челюскинцы живут на льду. Ночью прояснило. По звездам определили свое местонахождение: 67°17' с. ш., 172°51' з. д...» Как по этим данным найти на карте местоположение лагеря?

Прежде всего, уясним, через сколько градусов проведены параллели и меридианы на нашей карте. Допустим, они проведены через 5°. Значит, параллели и меридианы проходят через интервалы, кратные пяти градусам. Найдем на карте четырехугольник, ограниченный параллелями 65 и 70° с. ш. и 170 и 175° з.д. Переведем минуты заданных координат в десятые градуса, получим: В=67,3°; L= 172,8°. По меридианным сторонам четырехугольника отложим от основания отрезки, равные отношению (67,3-65)/5, т.е. 0,46 части стороны, и полученные точки соединим параллелью. На этой параллели от правого меридиана отложим отрезок, равный (172,8-170)/5=0,56 части отрезка параллели, и полученная точка укажет положение лагеря.

Долготу иногда выражают не в угловой мере, а во времени. Так как Земля поворачивается вокруг своей оси в 1 ч на 15° к востоку, то, когда в Гринвиче, откуда идет отсчет всемирного времени, полдень, в пункте, отстоящем от Гринвича на 30° к востоку, местное время будет 2 ч. Следовательно, долгота этого пункта соответствует двум часам. Долгота Харькова, например, равна

36°13'36" = 2 ч 24 мин 54,4 с к востоку от Гринвича.

Все меридианы сходятся у полюсов, и поэтому расстояние между двумя меридианами по мере их удаления от экватора уменьшается и на полюсах становится равным нулю. Отсюда следует, что протяженность дуги в 1° географической долготы на каждой параллели будет разной (табл. 3).

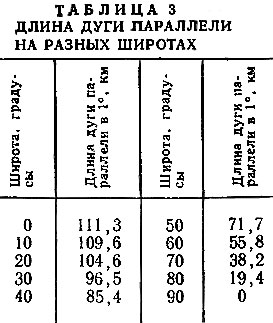
Длина дуги параллели на разных широтах

По данным этой таблицы построим график, по которому можно определять протяженность дуги параллели в 1° для любой широты. Чтобы график был компактным, покажем его с разрывами, ограниченными широтными интервалами от 0 до 10°, от 10 до 20°, от 20 до 30° и т. д. (рис. 33). Для этого сначала построим сетку квадратов. На вертикальной оси отложим и подпишем расстояния через 10 км, на горизонтальной оси - углы через 1°. Чтобы построить, например, линию, ограниченную широтным интервалом от 40 до 50°, нанесем по табличным данным две точки: первую для широты 40° (расстояние 85,4 км) и вторую для широты 50° (расстояние 71,7 км). Соединим эти точки линией, и она позволит нам определять протяженность дуги параллели в 1° на любой широте в пределах от 40 до 50°. Для широты 45°, например (точка А), протяженность дуги в 1° равна 79 км.

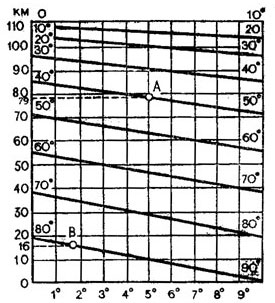
Рис. 33. График для определения протяженности дуги параллели в 1°

С помощью такого графика можно решать задачи, связанные с определением расстояний на земной поверхности. Необходимо иметь в виду, что расстояния по графику отсчитываются с точностью до 1 км, и поэтому окончательный результат может несколько отличаться от истинного.

Определим площадь острова Рудольфа, который расположен между 81,7° и 81,9° с. ш. и 58° и 59,2° в. д. Форма острова почти прямоугольная, и задача по сути дела сводится к определению протяженности его по широте и долготе.

Разность широт северной и южной оконечностей острова 0,2°. Известно, что дуга меридиана в 1° составляет примерно 111 км. Значит протяженность острова по широте равна 22 км (0,2 * 111). Так мы определили одну из сторон прямоугольника. Чтобы определить вторую сторону, найдем по графику длину дуги в 1° долготы на средней параллели острова, т. е. на широте 81,8°. Она получилась равной 16 км (см. точку В на графике). По долготе остров простирается на 1,2°. Значит, расстояние между восточной и западной его оконечностями равно примерно 19 км (16*1,2). Следовательно, площадь составит 418 км² (22*19).