ИСТИННЫЙ КОЭФФИЦИЕНТ

Расстановка ударений: И`СТИННЫЙ КОЭФФИЦИЕ`НТ

ИСТИННЫЙ КОЭФФИЦИЕНТ еcтественного прироста нас., собственный коэффициент естественного прироста, коэффициент прогрессивности режима воспроиз-ва, коэффициент Лотки, коэфф. естеств. прироста стабильного населения, соответствующего данному режиму воспроиз-ва нас. И. к.- средство анализа демографич. ситуации путём проекции её на будущую динамику нас. С этой целью, наряду с И. к. (r), рассматривают истинные коэфф. рождаемости (b) и смертности (m), равные соответств. характеристикам стабильного нас.: r = b-m.

Из теории стабильного нас. следует, что любое нас., в к-ром возрастные интенсивности рождаемости и смертности остаются неизменными, по истечении конечного промежутка времени превращается в стабильное, причём общий коэфф. естеств. прироста, пройдя ряд разл. значений, превращается в И. к., являющийся одной из интегральных характеристик режима воспроизводства населения. Понятие И. к. введено А. Лoткой. В совр. заруб. лит-ре пользуются терминами intrinsic [rate] (англ.), intrmseque (фр.) - 'собственный', 'внутренне присущий'; реже - true (англ.) - 'истинный'.

Для нахождения И. к. с данной женской функцией дожития l^F(x) и функцией рождаемости f(x) необходимо (приближённо) решить уравнение

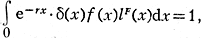
где δ(x) - доля девочек среди новорождённых в зависимости от возраста матери. Данное уравнение обладает единственным действительным корнем, т. е. для каждой пары f(x) и l^F(x) существует один и только один И. к. Для решения уравнения обычно используется разложение функции e^-rx в ряд Тейлора с той или иной точностью. При этом полагают, что δ не зависит от возраста матери. В первом приближении r = (ln R₀)/T, где R₀ - нетто-коэфф. воспроиз-ва:

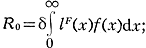
Т - средний возраст матери при рождении ребенка Т = R₁/R₀,

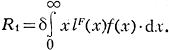
Более точно r может быть найден как корень квадратного уравнения

1/2βr² + Tr - ln R₀ = 0,

где β = (R₁/R₀)² - R₂/R₀;

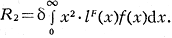
Указанные интегралы вычисляются с помощью обычных методов численного интегрирования.

В дискретной модели И. к. находится как логарифм положительного собственного числа λ матрицы воспроиз-ва: r = lnλ, где λ определяется условием: существует вектор Р, такой, что А*Р = λ*Р, где А - матрица воспроиз-ва (см. Модели воспроизводства населения).

В отличие от коэфф. естеств. прироста - меры изменения числ. конкретного нас., И. к. не зависит от существующей возрастной структуры нас. и измеряет совокупное влияние только режима рождаемости и порядка вымирания на динамику числ. нас. В стационарном нас. при r=0 (простое воспроиз-во) происходит количеств, замещение родительских поколений поколением детей; в стабильном нас. при r<0 (суженное воспроиз-во) количеств. замещение поколений не обеспечивается; при r>0 (расширенное воспроиз-во) числ. нас. от поколения к поколению возрастает. Применительно к реальному нас. указанные соотношения характеризуют не действит. меру роста его числ. в момент наблюдения (для к-рого рассчитан И. к.), т. к. возрастная структура реального нас., сложившаяся под воздействием режима воспроиз-ва в прошлом, обычно не соответствует возрастной структуре стабильного нас., а гипотетич. ситуацию, возможную лишь при условии сохранения в течение достаточно длит, времени неизменного режима воспроиз-ва, т. е. неизменных возрастных интенсивностей рождаемости и смертности. И. к., как правило, не равен фактически наблюдающемуся коэфф. естеств. прироста. Так, в 1969-70 в СССР И. к. составлял 4,5^o/oo, а общий коэфф. естеств. прироста - 9,0^o/оо.

Андреев Е., Пирожков С., О потенциале демографического роста, в кн : Население и окружающая среда, М. 1975; Lotka A. J., Relation Between Birth Rates and Death Rates, 'Science', 1907, v. 26; Dublin L. I., Lotka A. J., On the True Rate of Natural Increase of a Population, 'Journal of the American Statistical Association', 1925, v. 20.

Е. M. Андреев.

Источники:

1. Демографический энциклопедический словарь/Гл.ред. Валентей Д.И. М.:Советская энциклопедия - 1985