Измерение расстояний и площадей

Если вы собрались в многодневный поход, без карты, ие обойтись. Прежде всего, нужно узнать расстояние от начального до конечного пункта. Без этого нельзя рассчитать время похода и наметить остановки в пути. Сделать это нетрудно. Найдем на карте пункты, измерим циркулем или линейкой расстояние между ними, приложим этот отрезок к линейному масштабу и получим расстояние в километрах. Но ведь вы пойдете или поедете не по прямой линии, а по извилистым дорогам! Как же в таком случае измеряют расстояние?

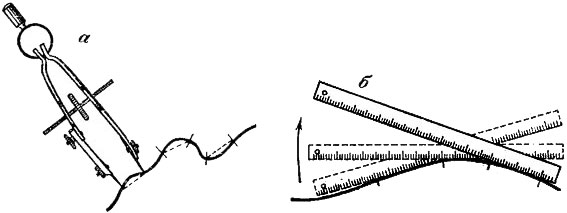
Рис. 34. Способы измерения расстояний: а — циркулем-измерителем; б — линейкой

Приближенный результат можно получить с помощью курвиметра, но для точных измерений он мало пригоден. Хорошо использовать циркуль-измеритель с малым раствором, который называют шагом. Одну иглу циркуля ставят в начальную точку, а вторую - на измеряемую линию (рис. 34, а). Поворачивая циркуль вокруг одной из игл, «шагают» по маршруту. Общая длина его равна числу шагов, умноженному на величину шага циркуля, плюс остаток, измеренный по линейному масштабу. Лучше всего пользоваться измерителем с микрометренным винтом. Он более точно удерживает раствор циркуля.

Если кривые плавные, то их разбивают на ряд отрезков, достаточно малых, чтобы можно было пренебречь разницей между длиной хорды и длиной дуги в каждом из них. Измерение криволинейной линии при этом сводится к измерению ломаного контура. Можно также непосредственно прикладывать к пологой кривой линии масштабную линейку, поворачивая ее по линии так, чтобы линейка все время по возможности оставалась касательной к кривой (рис. 34,6). При этом надо следить, чтобы линейка поворачивалась только около линии, но ни в коем случае не скользила. Этот чрезвычайно простой и удобный способ при некоторой тренировке дает достаточно точные результаты.

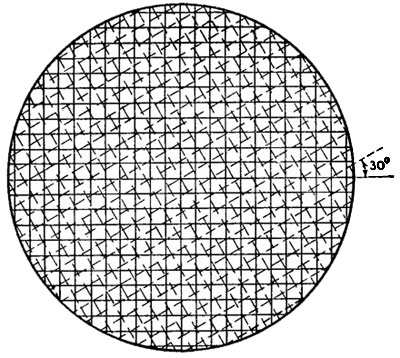
Рис. 35. Палетка для измерения расстояний по карте

По карте измеряют не только протяженность маршрута, но и длину реки, береговой линии озера, моря и других линейных географических объектов. И если измерений много, то целесообразно изготовить специальную палетку (рис. 35). Ее делают из прозрачной основы, на которую наносят разным цветом две сетки квадратов, расположенные относительно друг друга под углом 30°. Каждая сторона квадрата сеток равна 3,82 мм. При определении длины линии палетку накладывают на карту так, чтобы концы измеряемой кривой оказались внутри сетки. Подсчитывают число сторон квадратов, пересекаемых измеряемой линией, вначале по сетке одного цвета, а затем, не сдвигая палетки, - по сетке другого цвета. Вычисляют среднее арифметическое из отсчетов по двум сеткам, и утроенное значение полученной величины даст длину измеряемой линии в миллиметрах.

Можно обойтись и одной сеткой, но в таком случае счет пересечений ее сторон с измеряемой линией придется вести при двух ее положениях. Вначале сетку располагают так, чтобы ее стороны были параллельны рамкам карты, а затем сетку поворачивают примерно на 30°. Если же отсчеты произвести при трех положениях сетки, т.е. после первого поворота, повернуть ее еще раз на 30°, то суммарное число пересечений даст искомую длину линии в миллиметрах.

Измерения расстояний производят по картам, на которых искажений нет или они практически незаметны. К ним относятся, прежде всего, топографические карты, а также карты районов, областей, краев, союзных республик, отдельных государств, протяженность которых с юга на север или с востока на запад не превышает 1500-2000 км. Но даже и на таких картах, как бы точно ни измеряли расстояния, они не будут соответствовать истинным. Это происходит потому, что в результате картографических обобщений извилистые линии на картах бывают укорочены по сравнению с реальными. На топографической карте, например, масштаба 1:200000 несоответствие достигает 25 %.

Измерять расстояния на мелкомасштабных картах сложнее, чем на крупномасштабных, так как приходится считаться с переменным масштабом. Однако во многих случаях частные масштабы по всей карте или хотя бы на некоторых участках ее настолько мало отличаются от главного масштаба, что с достаточной для практики точностью масштаб считают постоянным. Наиболее точно длину по мелкомасштабной карте можно определить, если расстояние между точками измеряют по меридиану или по параллели. Определив разность широт или долгот начальной и конечной точек, умножают ее величину на длину дуги в 1° по меридиану или параллели и получают заданное расстояние. В качестве примера определим протяженность Каспийского моря с юга на север по меридиану 50°. Для этого определим по карте географические широты точек пересечения береговой линии моря с пятидесятиградусным меридианом. Они получились равными 46,5 и 37,5° с. ш. Разность их составляет 9°, что соответствует расстоянию 999 км (9* 111).

Это расстояние (округленно 1000 км) соответствует длине Каспийского моря от устья Волги до берегов Ирана. Его можно использовать при изучении Европы и Азии в качестве сравнительного эталона для глазомерной оценки расстояний между различными пунктами. Подобные эталоны можно наметить и для других стран мира. Например, для Африки - длина Красного моря - 2000 км, для Северной Америки - длина полуострова Калифорния - 1200 км, для Австралии - длина мыса Йорк - 800 км.

На морских картах, которые строятся в проекции Меркатора, не дается линейный масштаб. Его роль выполняют восточная или западная стороны рамки карты, представляющие собой меридианы, разбитые на деления через 1' по широте. У моряков расстояния принято оценивать в милях. Морская миля - это средняя длина дуги меридиана в 1' по широте, равная 1852 м. Таким образом, рамки морской карты фактически разбиты на морские мили. Определив расстояние между двумя точками на карте в минутах меридиана, получают действительные расстояния в морских милях.

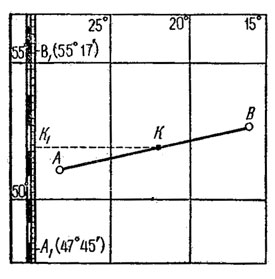
Рис. 36. Схема определения расстояний на морской карте

Если точки А и В расположены не на одном меридиане (рис. 36), то раствор циркуля-измерителя нужно перенести на рамку так, чтобы обе иглы циркуля отстояли на одинаковых расстояниях от концов проекций измеряемой линии. Для этого вначале намечают в середине отрезка точку К и проектируют ее на боковую сторону рамки. От этой точки К₁ откладывают отрезки К₁А₁ и K₁B₁, равные отрезкам КА и КВ. Расстояние АВ в милях равно разности отсчетов широт точек А₁ и В₁. В нашем случае оно получилось равным 452 милям (55°17'-47°45'=7°32'=452').

Если предстоит длительная работа с мелкомасштабной картой, то имеет смысл изготовить специальный масштаб для измерения расстояний по разным параллелям. Образец такого масштаба приведен на рис. 37. Он представляет собой совокупность нескольких линейных масштабов, каждый из которых начерчен для соответствующего частного масштаба карты по различным параллелям. На нашем чертеже такие масштабы построены через 20° по широте. Нижняя горизонтальная линия соответствует масштабу на экваторе, следующая за нею Ч частному масштабу на параллели 20° и т. д. Отдельные точки масштаба соединяются плавными кривыми, что дает возможность измерять по масштабу длины линий, лежащих на промежуточных широтах.

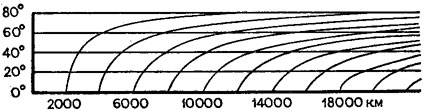
Рис. 37. Масштаб для измерения расстояний по разным параллелям

Карта позволяет ответить и на такие вопросы, как, например, сколько гектаров занимает озеро, на какой площади раскинулся город и т. п. Наиболее просто и быстро площадь по карте можно определить графическим путем. На контуре, в пределах которого требуется определить площадь, на глаз строят равновеликий прямоугольник (рис. 38, а). Измерив его основание а и высоту b и перемножив одно на другое, получим площадь фигуры. Для более точных определений фигуру разбивают на сеть прямоугольников, квадратов и треугольников. Площадь каждого из них вычисляют по известным правилам геометрии. Сумма площадей отдельных фигур даст общую площадь, заключенную в контуре.

Очень удобно определять площадь по сетке квадратов, нанесенной на прозрачную бумагу или пленку. Стороны квадратов должны быть такими, чтобы каждый из них соответствовал целому числу гектаров или квадратных километров. Так, для карт масштабов 1:25000, 1:250000 и 1:2500000 квадрат вычерчивают со стороной 4 мм. Для первой карты один квадрат будет соответствовать 1 га, для второй - 1 км² и для третьей - 100 км².

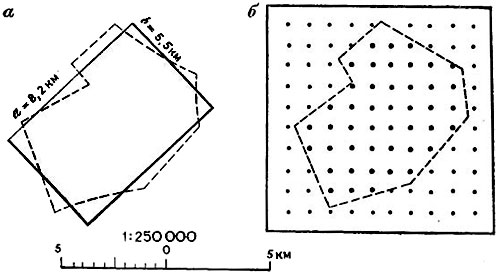
Рис. 38. Схема определения площади: а — построением равновеликого прямоугольника; б — точечной палеткой

Накладывая такую сетку на карту, подсчитывают число квадратов, покрывающих площадь, причем доли квадратов определяют на глаз. Вместо сетки квадратов можно ограничиться только точками, отмеченными в вершинах квадратов (рис. 38, б); Количество точек в пределах контура будет соответствовать числу квадратов, и здесь уже не нужно подсчитывать число долей квадратов. В нашем случае на изображение контура попало 45 точек, значит, площадь, заключенная в нем, составляет 45 км².

Для точного измерения площадей применяют специальный прибор - планиметр. Простейший планиметр-топорик можно легко изготовить самому. Он состоит из металлического стержня, согнутого в виде широкой буквы П (рис. 39). Один конец инструмента расплющивается в виде топорика, а другой - ведущий конец заостряется в иглу. Для правильного измерения площади необходимо, чтобы острие иглы лежало в плоскости, проходящей через лезвие топорика; во время работы инструмент должен быть в вертикальном положении.

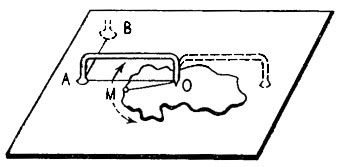
Рис. 39. Схема измерения площади планиметром-топориком

Для определения площади какой-либо фигуры намечают на глаз ее центр тяжести - точку О и соединяют ее с точкой М, находящейся на контуре. Планиметр ставят острием в точку О и слегка нажимают на топорик, чтобы получить след на бумаге А. Затем иглой обводят занимаемую площадь, сначала по прямой ОМ до контура, далее делают полный оборот по контуру до точки М и, наконец, снова возвращаются в исходную точку О. После этого легким нажимом фиксируют на бумаге новое положение топорика В. Площадь, ограниченная контуром, равняется произведению длины планиметра АО на расстояние АВ между начальным и конечным положениями топорика: s=AO*AB.

Для уточнения результата и исключения ошибки от несовпадения точки О с центром тяжести фигуры надо повернуть инструмент на 180° и сделать новый обвод в противоположном направлении. За окончательный результат принимают среднее из двух значений. Планиметр-топорик очень прост в работе и может с успехом применяться для измерения площадей с точностью, не превышающей 2-3 %.

На мелкомасштабных обзорных картах, которые содержат большие искажения, площади можно определять по клеткам картографической сетки. Размеры площадей клеток выбирают из таблиц, которые можно найти почти в каждом географическом атласе, например в атласе для учителей. Частично занятые клетки, так называемые домерки, оценивают на глаз с точностью до десятых долей. Для большей точности клетки картографической сетки делят на более мелкие с таким расчетом, чтобы их площади можно было найти в таблицах.