Кратчайший путь на глобусе и карте

Мы знаем, что кратчайший путь между какими-либо двумя точками проходит по дуге большого круга, которая называется ортодромией. Ее можно построить с помощью глобуса. К намеченным на нем пунктам прикладывают нить, которая и соответствует ортодромии - дуге большого круга. Для переноса ее на карту определяют широты и долготы точек пересечения ортодромии с меридианами или параллелями. Запись координат можно вести в табличной форме. Дадим ее, например, для трассы Москва-Гавана.

Номера точек.. 1 2 3 4.

Долгота .... 30° в. д. 15° в. д. 0 15° з. д.

Широта ..... 58° с. ш. 61° с. ш. 62° с. ш. 61° с; ш.

Продолжение

Номера точек.. 5 6 7 8

Долгота .... 30° з. д. 45° з. д. 60° з. д. 75° з. д.

Широта ..... 59° с. ш. 54° с. ш. 46° с. ш. 32° с. ш.

По данным координатам наносят на карту точки и затем соединяют их плавной кривой линией. Эта линия является трассой кратчайшего воздушного пути самолетов, следующих из Москвы в Гавану и обратно.

Такую задачу можно решить и без глобуса, по карте северного или южного полушария. Допустим, нам требуется узнать кратчайший путь между городами Махачкала и Владивосток, широта которых почти одинакова (рис. 40, а). Возьмем циркуль и, передвигая его иглу вдоль линии меридиана, расположенного посередине между пунктами, подберем такой радиус, чтобы дуга окружности проходила через оба пункта и опиралась на диаметр полушария. Кратчайший путь в нашем примере проходит по дуге, показанной на рисунке утолщенной линией. Данный прием нанесения кратчайшего маршрута на карту полушария можно применить и для пунктов, имеющих различную долготу и различную широту. Однако в последнем случае подобрать радиус и найти центр окружности, дуга которой проходила бы через оба пункта и концы диаметра, не так-то легко. Значительно проще подобные задачи решать с помощью палетки, изготовленной из прозрачного материала (кальки, целлофана). Делается она так. Лист кальки накладывают на карту полушария и переносят на нее с карты полуокружность. Затем через равные промежутки строят дуги, соединяющие концы полуокружности (рис. 40, б).

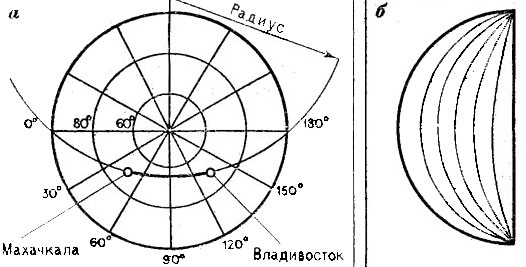
Рис. 40. Способ нахождения по карте полушария кратчайшего путь

Чтобы определить кратчайший путь между двумя пунктами, совместим линию полуокружности на палетке с линией окружности на карте. Поворачивая палетку вокруг центра полуокружности, добьемся такого положения, когда оба пункта окажутся на одной какой-либо дуге. По этой дуге и будет проходить кратчайший путь. Нужно только еще раз проверить точность совмещения линии на палетке с дугой окружности на карте.

Естественно, возникает вопрос: нет ли такой карты, на которой ортодромия изобразится в виде прямой? Есть такая карта. Она составлена картографами в азимутальной проекции, в которой проецирующие линии исходят из центра шара. В этом случае любое сечение шара, проходящее через центр, будет проектироваться на плоскость, касательную к поверхности шара, в виде прямой. Дело в том, что центр шара является одновременно центром любого сечения, делящего шар пополам, т. е. центром любого большого круга. При проецировании большого круга из центра шара мы получим безгранично расширяющуюся плоскость, которая, пересекаясь с плоскостью проекции, будет всегда давать прямую.

Ортодромия на карте показывает направление кратчайшего пути. Но по этому направлению масштаб будет отличаться от главного, который подписан на карте. Мало того, он будет разным в различных частях маршрута. Как же в таком случае определить расстояние по маршруту между начальным и конечным пунктами?

Оригинальный способ решения такой задачи предложил русский математик П. Л. Чебышев. Прежде всего, находят географические координаты пунктов, между которыми определяют расстояние. Затем вычисляют разности координат, не учитывая знаков, и разность широт умножают на 120, а разность долгот - на 60. Большее из полученных двух чисел умножают на 7, а меньшее - на 3. Складывают оба числа, сумму делят на 7,5, и в результате получают расстояние между пунктами в километрах.

В качестве примера определим расстояние между Москвой и Ленинградом по их координатам. Москва: 55,7° с. ш., 37,5° в. д.; Ленинград: 59,9° с. ш., 30,3° в. д.

55,7° - 59,9° = 4,2*120 = 504*7 = 3528; 37,5° - 30,3° = 7,2*60 = 432*3 = 1296.

Сумма полученных чисел равна 4824. При делении этого числа на 7,5 получим расстояние между Москвой и Ленинградом, равное 643 км.

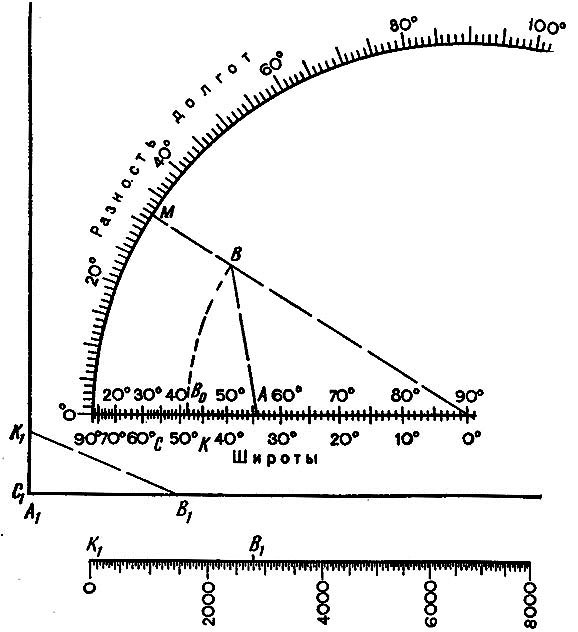
Рис. 41. График для определения расстояний между пунктами

Данный способ приближенный. Более точные результаты можно получить по номограмме (рис. 41). Порядок работы с помощью номограммы рассмотрим на следующем примере.

Определить расстояние между Москвой и Ташкентом по их координатам (Ташкент: 41,3° с. ш., 69,3° в. д.).

1. На круговой шкале отметим разность долгот пунктов 31,8° и соединим полученную точку М с центром круговой шкалы.

2. На верхней горизонтальной широтной шкале отложим точки А и В_о, соответствующие широтам пунктов, и проведем из центра О дугу радиусом ОВ₀. При пересечении с линией ОМ отметим точку В и соединим ее с точкой А.

3. На нижней широтной шкале отметим точки С и K, также соответствующие широтам пунктов.

4. На сторонах прямого угла отложим отрезки С₁К₁ и A₁B₁, равные соответственно СK и АВ. Отрезок K₁B₁ является гипотенузой прямоугольного треугольника.

5. Отложим отрезок K₁B₁ на самой нижней шкале и получим ответ: расстояние между пунктами равно 2800 км.

При тщательной работе с циркулем-измерителем расстояния с помощью увеличенной номограммы можно определять с точностью до 10 км.